こんにちはー、ウチダです!
金(GOLD)を2000年から2012年まで保有していたら、価格が6倍になった事実を知っていますか?
実は、金はトレンドを知ると、大きく儲けられる資産なのです!
今回はプログラミングで金の投資分析をした話を紹介します。
★銀の投資分析をプログラミングでした話はこちら
目次
金は儲かる!おすすめの投資方法

金投資とは、金(GOLD)に投資することです。
金の価格は常に動いており、売買時の価格差を使って利益を得ます。
まずは金の特徴を説明します。
金の需要は宝飾品がメイン

金の統計情報はGOLD HUBにたくさん載っています。
例えば、金の需要を調べると、約半分以上は宝飾品に使われていることがわかります。
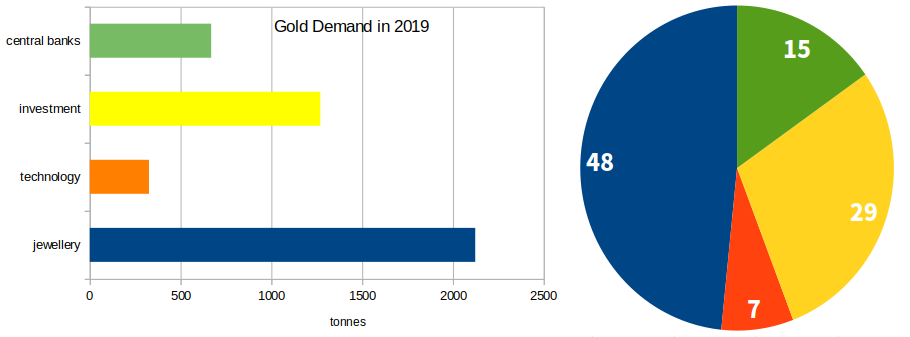
(引用:GOLD HUB、「Gold supply and demand statistics」:リンク)
四半期ごとの金の需要も調べることができます。
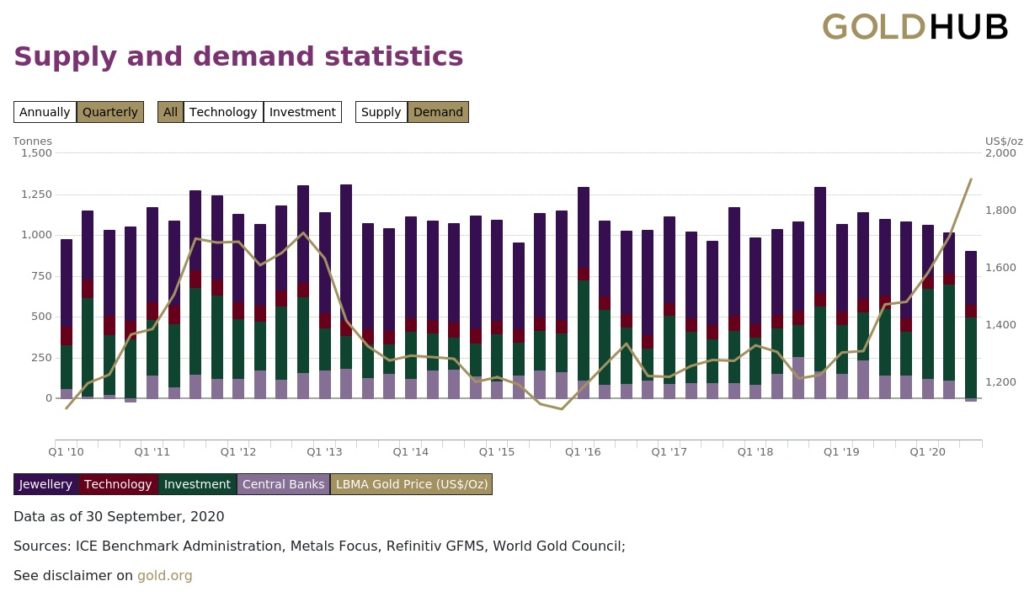
(引用:GOLD HUB、「Gold supply and demand statistics」:リンク)
図2で、面白いことに気づきませんか?
それは、金の価格が上昇したとき、投資用の金の需要が高まっていることです。
宝飾品の需要が約半分も占めているのに、価格には投資用途が影響するのは面白いです。
さらに投資用の内訳まで表示できます。
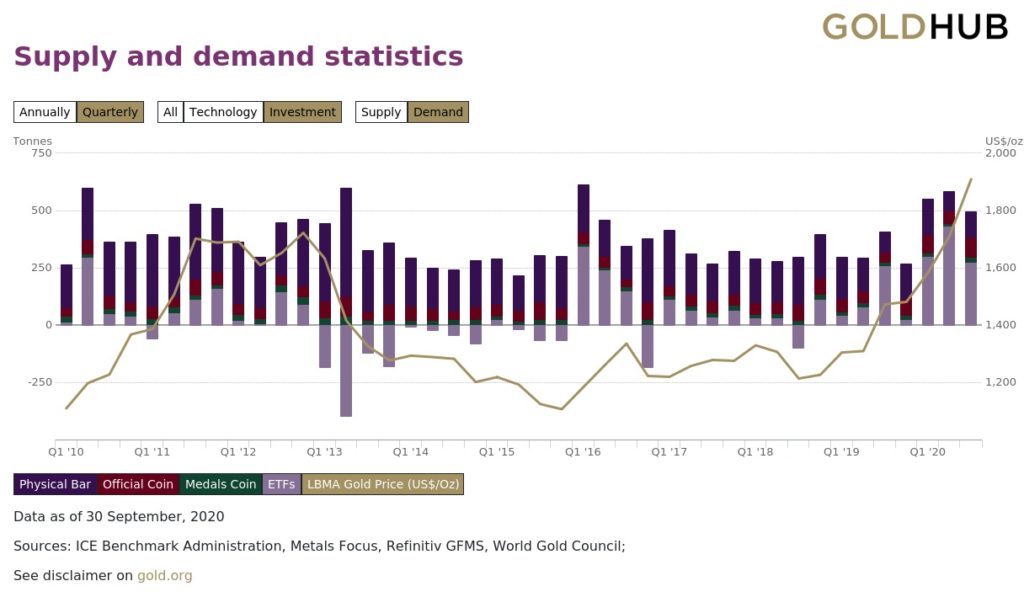
(引用:GOLD HUB、「Gold supply and demand statistics」:リンク)
2010年頃のリーマンショックと2020年のコロナショックは、どちらも金の価格が上昇しています。
しかし、需要の中身に大きな違いがあります。
2010年頃のリーマンショックでは実物(延べ棒)が大きく伸びました。
一方、2020年のコロナショックでは金ETFの需要が大きく伸びています。
この違いは何でしょう?
ぼくは投資コストを考えているのだろうと見ています。
これは後ほど説明します。
価格に影響にはドル安が影響する

そもそも金の価格に影響する因子には次の5つが挙げられます。
- 需要と供給のバランス
- 米ドルの価値
- 地政学リスク
- インフレ
- 各国中央銀行の売買動向
私が注目しているのは、米ドルの価値です。
ここでは米ドルの価値をマネタリーベースで考えます。
(参考:マネタリーベースとは?)
2008年にアメリカは量的金融緩和を行い、大量の米ドルを発行しました。
供給が多くなるので、米ドルの価値は下がります。
つまりドル安に向かいます。
このとき、金の価格はどうなったのでしょう?
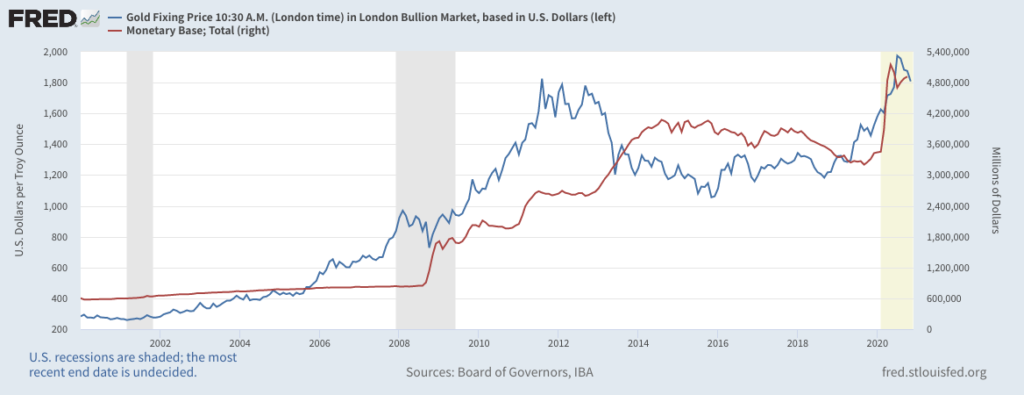
マネタリーベースの急増に合わせて、金が暴騰しています。
2000年を基準にすると、2012年には6倍の価格です。
なぜ金が暴騰しているのか?
米ドルの価値で考えます。
下図は10年国債の利回りとインフレ率を比較したものです。
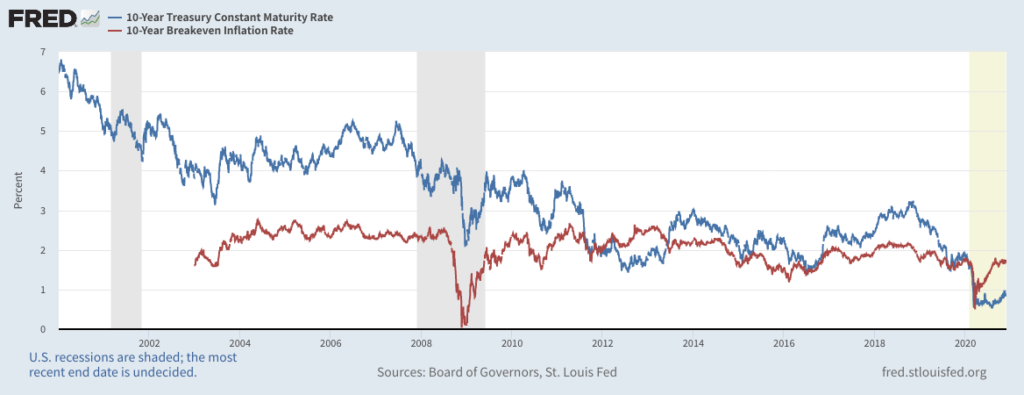
この国債利回りは名目金利とも呼ばれます。
国債でどれだけお金が増えるのか表す指標です。
これに対してインフレ率は、どれだけ物価が上がるかの指標です。
利回りが大きくても、物価がそれ以上に上がれば、事実上お金は目減りしています。
これが、実質金利です。
実質金利は、名目金利(10年国債の利回り)からインフレ率を差し引いた指標です。
実質金利と金の価格との関係はこのようになります。
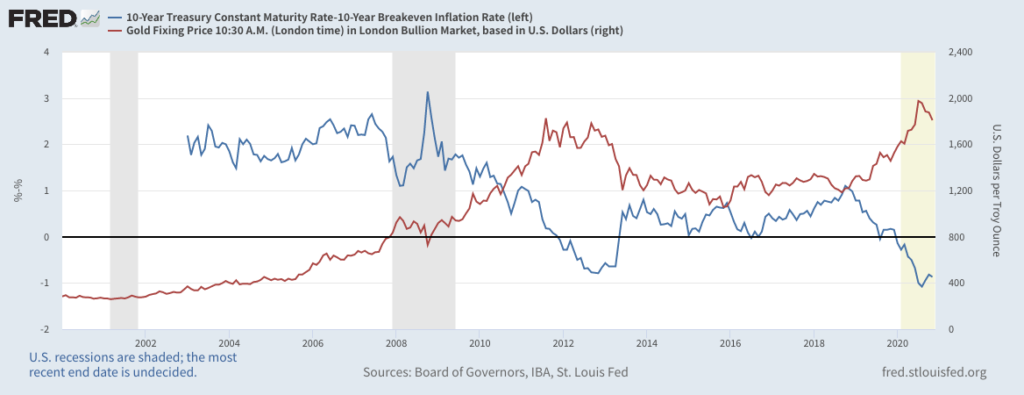
実質金利が下がる(お金の価値が目減りする)と、金の価格が上昇しています。
これは、お金の価値が下がると、物の価値が上がることを表しています。
ここでは、物=金となるわけです。
ちなみに、2013年頃は金の価格が下落していますが、これも米ドルの価値が関係しています。
- 欧州債務危機でユーロ安が進んだ。
- 日本が量的金融緩和を始めたので円安ドル高が進んだ。
- FOMCで量的金融緩和の縮小を支持する意見が顕著になってきた。
(参考:日経新聞、ドル安時代の終わりを告げる金暴落:リンク)
実際、金の需要推移を見ても、2013年頃に金ETFから資金が流出しています。

(参考:GOLD HUB、Gold supply and demand statistics:リンク)
金に投資をするなら、米ドルの価値を注視する必要があるでしょう。
金へのおすすめの投資方法は?

個人投資家が金に投資する方法として、今回は純金積立と金ETFを取り上げます。
どちらも金の価格の動きを利用して利益を得る投資法です。
ここでは、コスト面でどちらの投資がおすすめなのかシミュレーションで示します。
まず純金積立にかかるコストは次の通りです。
- 買付時に購入代金の2.2%
- 保有期間が5年以内で売却すると、短期譲渡所得がかかる
- 保有期間が5年超で売却すると、長期譲渡所得がかかる
次に金ETFにかかるコストは、SPDRゴールドシェア(1326)を参考にします。
- 買付け時に手数料がかかる(5万円までは55円)
- 信託費用0.4%(年間コスト)
- 売却時に利益に対して20.315%課税
- (参考:SPDRゴールドシェア(1326):リンク)
この条件で、毎月1万円を40年間(合計480万円)積立投資した場合と、
一括で480万円投資して40年間保有していた場合のコストを比較します。
なお、金の価格は変化がないものとしてシミュレーションします。
まずは積立投資の場合です。
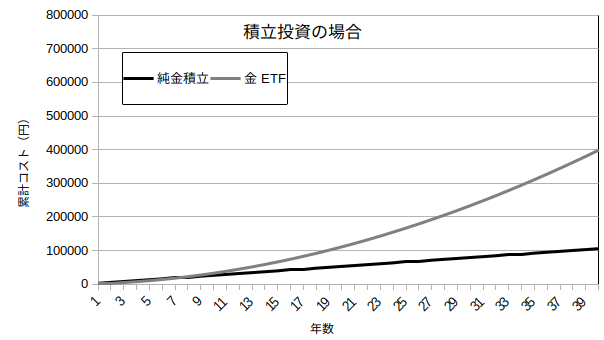
シミュレーションの結果、9年以下の短期投資であれば金ETFのほうがコストが低く、
それ以上の期間であれば積立投資のほうが低いです。
次に一括投資の場合です。
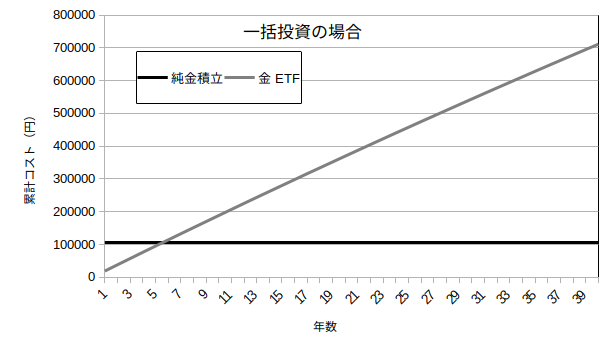
シミュレーションの結果、5年以下の短期投資であれば金ETFのほうがコストが低く、
それ以上の期間であれば積立投資のほうが低いです。
また、積立投資の場合と比較して、金ETFはコストがかなり大きくなっています。
これは信託報酬が累計投資額の0.4%が影響しています。
一括投資だと最初から投資額が大きい分、信託報酬の額が大きくなっているのです。
40年後のコストを比較すると、次のようになります。

短期の値動きで利ざやを狙うなら金ETFがよいでしょう。
一方、長期投資を考えるなら、純金積立のほうが好ましいでしょう。
余談ですが、リーマンショックとコロナショックにおける金の投資需要が異なることもコストに関係していると考えています。
リーマンショックでは、初めて量的金融緩和を行うこともあり、先行きが不透明でした。
そこで、長期投資を考えて、金の実物の需要が増したと推測しています。
一方、コロナショックは、金ETFの需要が大きく増していることから、短期投資が狙われていると推測します。
量的金融緩和で価格が上昇した後、5年程度で売りが大量に発生し、価格が下がるのではないでしょうか?
金を投資のポートフォリオに入れよう

一般的に、リスクを分散させるために、投資対象は多いほうがいいです。
ただし、相関が高い資産を組み合わせてもリスクは分散できません。
そこで、金の価格と株価に相関があるのか調べます。
株式と金との相関を調べる

米国の株価の指標としてS&P500と金の価格の関係を調べます。
まず値動きを比較すると、このようになります。
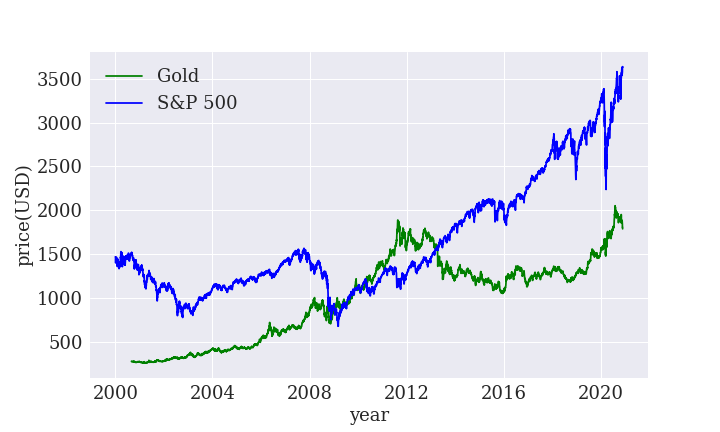
どちらの方が儲かるかというと、圧倒的に金です。
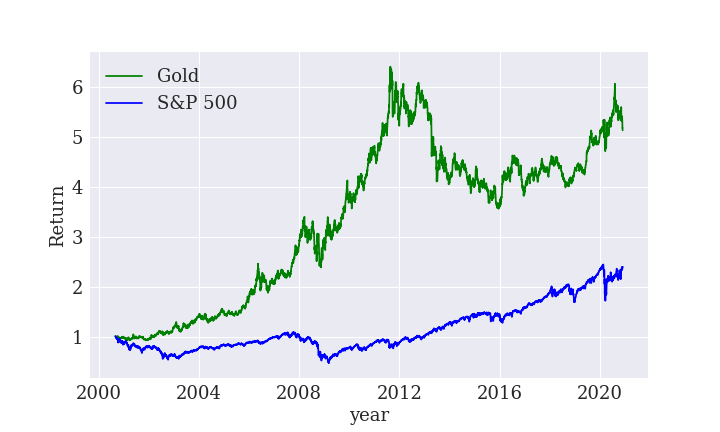
Y軸のリターンは、2000年1月1日の価格を基準に何倍になったかを示しています。
2000年から2012年にかけて、金は6倍に暴騰しています。
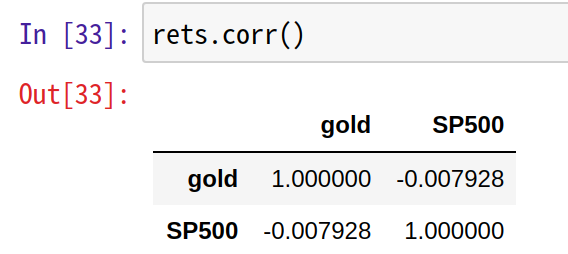
次に相関を調べます。
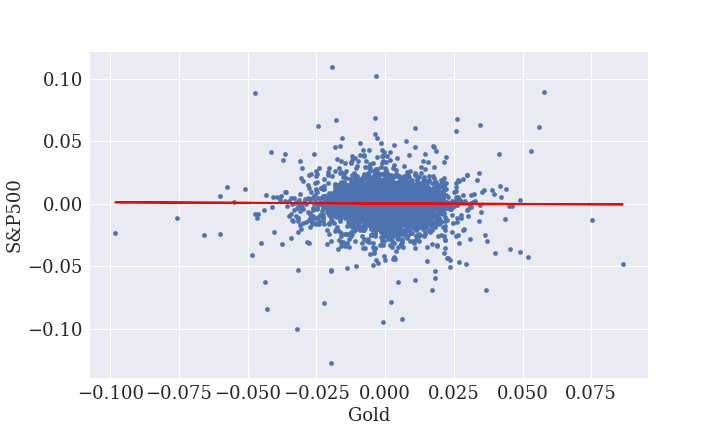
S&P500と金の価格に相関は見られません。
相関尺度も低く、株と金の組み合わせは分散投資として有効です。
株式と金でおすすめのポートフォリオを作成する

S&P500と金に投資する場合の最適な比率を考えます。
株価も金の価格も変動率が正規分布に従いませんが、参考までに効率的フロンティアを作成します。
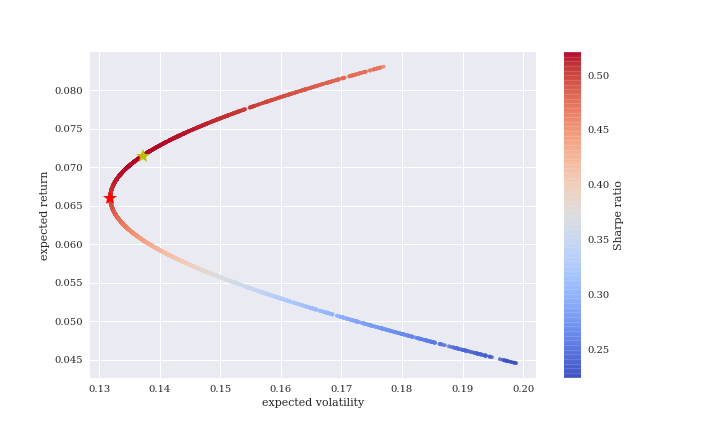
今回は投資商品が2つなので、曲線になりました。
赤色星は最もリスクが小さくなる点です。
構成比率は以下になります。
- 期待リターン:6.6%
- 期待ボラリティ:13.2%
- S&P500:44.2%
- 金:55.8%
次にシャープレシオが最も高い点(黄色星)を見ます。
シャープレシオは、期待リターンを期待ボラリティで割ったもので、投資効率の指標です。
- 期待リターン:7.2%
- 期待ボラリティ:13.7%
- S&P500:30%
- 金:70%
あくまで参考程度ですが、ぜひ投資の参考にしてください!
まとめ
今回は金投資を説明しました。
金はインフレ対策や分散投資に有用なので、ぜひ投資対象に入れましょう。
ここまで読んでくださりありがとうございました。
Pythonプログラムのコード

今回使用したPythonコードを以下に示します。
投資とプログラミングの組み合わせに興味があればぜひ活用してください!
価格チャートをpythonで表示する

Yahoo! financeからデータを取得しています。
S&P500は^GSPC、金はGC=Fを使用しています。
#import libraries
from pandas_datareader import data
import pandas as pd
from pylab import mpl, plt
import numpy as np
import datetime
plt.style.use('seaborn')
mpl.rcParams['font.family'] = 'serif'
%matplotlib inline
#date
start = '2000-01-01'
end = datetime.date.today()
#get date from yahoo! finance
def price_df(item, start, end):
file = data.DataReader(item, 'yahoo', start, end)
date = file.index
price = file['Close']
return date, price
#S&P 500 price
SP500_date, SP500_price = price_df('^GSPC', start, end)
#Gold price
gold_date, gold_price = price_df('GC=F', start, end)
#show a price chart
plt.figure(figsize=(10, 6))
plt.plot(gold_date, gold_price, label = 'Gold', color='g')
plt.plot(SP500_date, SP500_price, label = 'S&P 500', color='b')
plt.legend(loc=2, fontsize=18)
plt.xlabel('year', fontsize=18)
plt.ylabel('price(USD)', fontsize=18)
plt.tick_params(labelsize=18)
plt.savefig("SP500_gold_1.png")リターンをpythonで比較する

対数収益率でリターンを計算しています。
最初の値を基準にloge(Pn/Pn-1)で計算します。
合計は、loge(Pn/P1)となります。
これをexpの指数に入れることで、Pn/P1が得られます。
つまりリターンは、最初の値の倍数になります。
#make a DataFrame
df = pd.DataFrame()
df['gold'] = gold_price
df['SP500'] = SP500_price
#calculate log returns
rets = np.log(df / df.shift(1))
rets.dropna(inplace=True)
return_date = rets.index
gold_return = rets['gold'].cumsum().apply(np.exp)
SP500_return = rets['SP500'].cumsum().apply(np.exp)
#show a return chart
plt.figure(figsize=(10, 6))
plt.plot(return_date, gold_return, label = 'Gold', color='g')
plt.plot(return_date, SP500_return, label = 'S&P 500', color='b')
plt.legend(loc=2, fontsize=18)
plt.xlabel('year', fontsize=18)
plt.ylabel('Return', fontsize=18)
plt.tick_params(labelsize=18)
plt.savefig("SP500_gold_2.png")相関関係をpythonで調査する

価格の変動率をlogで算出し、散布図にプロットすることで相関を調べます。
#OLS analysis
reg = np.polyfit(rets['gold'], rets['SP500'], deg=1)
#scatter plot
ax = rets.plot(kind='scatter', x='gold', y='SP500', figsize=(10,6), fontsize=18)
ax.plot(rets['gold'], np.polyval(reg, rets['gold']), 'r', lw=2)
plt.xlabel('Gold', fontsize=18)
plt.ylabel('S&P500', fontsize=18)
plt.savefig("SP500_gold_3.png")
#correlation
rets.corr()効率的フロンティアをpythonで作成する

今回は投資先が2つだったので、曲線になりました。
金とS&P500の比率を変えて、リスクとリターンの関係を調べています。
シャープレシオは、期待リターンを期待ボラリティで割ったもので、投資効率の指標です。
シャープレシオが高い(赤色が濃い)ほど、効率のよい投資ができます。
#import libraries
import math
import scipy.stats as scs
import statsmodels.api as sm
#number of item to invest
noa = 2
#calculate return
def port_ret(weights):
return np.sum(rets.mean() * weights) * 252
#calculate volatility
def port_vol(weights):
return np.sqrt(np.dot(weights.T, np.dot(rets.cov() * 252, weights)))
#make plot data
prets = []
pvols = []
for p in range(2500):
weights = np.random.random(noa)
weights /= np.sum(weights)
prets.append(port_ret(weights))
pvols.append(port_vol(weights))
prets = np.array(prets)
pvols = np.array(pvols)
#import libraries
import scipy.optimize as sco
#calculate sharp ratio
def min_func_sharpe(weights):
return -port_ret(weights) / port_vol(weights)
#restriction
cons = ({'type':'eq', 'fun':lambda x: np.sum(x) - 1})
bnds = tuple((0, 1) for x in range(noa))
#initial raio
eweights = np.array(noa * [1. / noa,])
#calculate the best value of sharp ratio
%%time
opts = sco.minimize(min_func_sharpe, eweights,
method='SLSQP', bounds=bnds,
constraints=cons)
#the result of calculation
opts['x'].round(3)
port_ret(opts['x']).round(3)
port_vol(opts['x']).round(3)
port_ret(opts['x']) / port_vol(opts['x'])
#calculate minimum volatility
optv = sco.minimize(port_vol, eweights,
method='SLSQP', bounds=bnds,
constraints=cons)
#the result of calculation
optv['x'].round(3)
port_vol(optv['x']).round(3)
port_ret(optv['x']).round(3)
port_ret(optv['x']) / port_vol(optv['x'])
#show a efficient frontier
plt.figure(figsize=(10, 6))
plt.scatter(pvols, prets, c=prets / pvols,
marker='.', alpha=0.8, cmap='coolwarm')
plt.plot(port_vol(opts['x']), port_ret(opts['x']),
'y*', markersize=15.0)
plt.plot(port_vol(optv['x']), port_ret(optv['x']),
'r*', markersize=15.0)
plt.xlabel('expected volatility')
plt.ylabel('expected return')
plt.colorbar(label='Sharpe ratio')
plt.savefig("SP500_gold_5.png");投資とプログラミングの組み合わせに興味があればぜひ声をかけてくださいね。
ここまで読んでくださりありがとうございました。^^
★プログラミング言語pythonによる投資の分析に役立つ本

