こんにちはー、ウチダです!
銀(SILVER)を2000年から2011年まで保有していたら、価格が10倍になった事実を知っていますか?
実は、銀は金より大きく儲けられる資産なのです!
今回は銀投資についてお話します。
銀投資は儲かる!ブログで徹底解説

銀投資とは、銀(SILVER)に投資することです。
銀の価格は常に動いており、売買時の価格差から利益を出します。
まずは銀の特徴を説明します。
銀の需要は工業製品がメイン

銀の統計情報はSILVER INSTITUTEにたくさん載っています。
例えば、銀の需要を調べると、約半分以上は工業製品に使われていることがわかります。
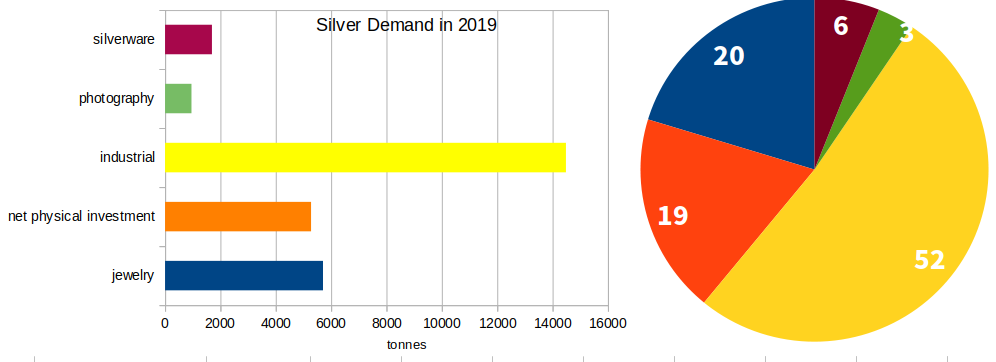
(引用:The Global Source THE SILVER INSTITUTE、「SILVER SUPPLY & DEMAND」:リンク)
また、直近9年間の需要と価格の傾向は以下のとおりです。
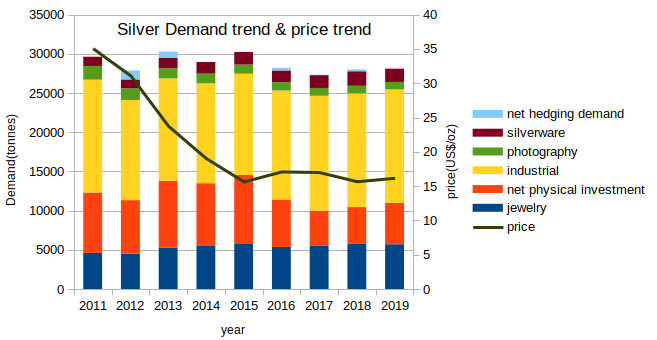
(引用:The Global Source THE SILVER INSTITUTE、「SILVER SUPPLY & DEMAND」:リンク)
金とは違って、投資用の需要と価格に相関がありません。
銀の価格には何が影響しているのでしょう?
価格にはドル安が影響する

銀の価格に影響する因子には次の5つが挙げられます。
- 需要と供給のバランス
- 景気動向
- 金価格との比較
- インフレ
- 地政学リスク
今回は金価格との比較に着目します。
まず金との相関を調べると、かなり高いことがわかります。
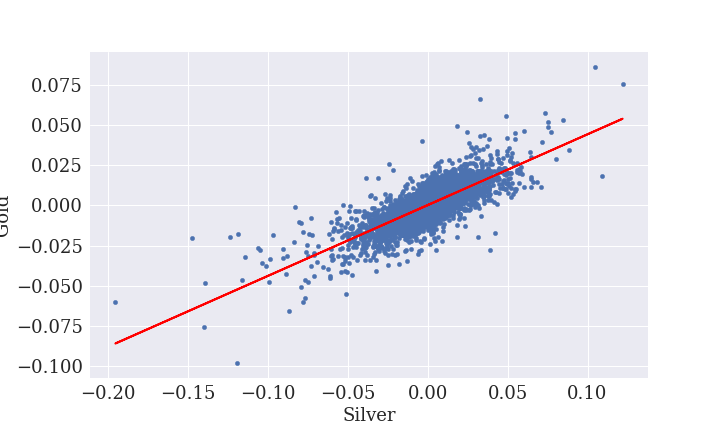
相関尺度も約0.8あり、金と銀は相関が高いといえます。

金の価格は実質金利と逆相関があります。(参考:金の価格に影響するものは?)
銀も同様なのか確認しましょう。
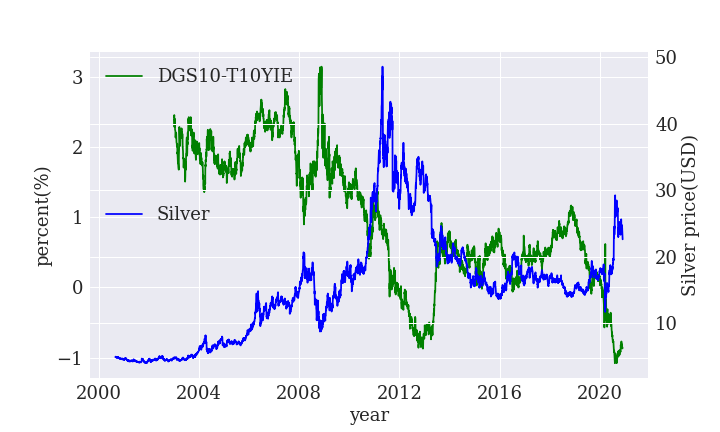
実質金利が下がる(お金が目減りする)と、銀の価格が上昇しています。
これは、お金の価値が下がると物(=銀)の価値が上がることを表しています。
金と銀の価格を比較する

金と銀の価格を比較する指標として、Gold Silver Ratioがあります。
(参考:Gold Silver Ratioとは?)
金の価格を銀の価格で割ることで比率を計算します。
この比率が大きくなれば、金が割高、銀が割安と考えられます。
Gold Silver Ratioによって金や銀の売買が判断されることがあります。
では、直近20年間の金(紫色)と銀(緑色)の価格と、Ratio(赤色)を見てみましょう。
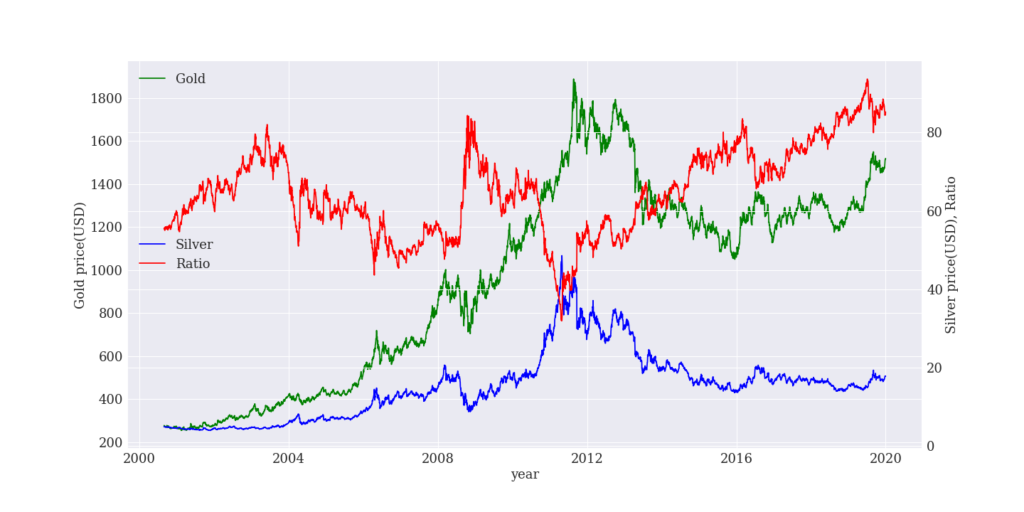
Ratioはだいたい50〜80程度で動いているように見えます。
2019年にこのレンジを突破しましたが、2020年の秋頃には80まで戻ってきました。
仮にこの50〜80のレンジで動くなら、今後はRatioが下がるはずなので、金の価格が下がるか、銀の価格が上がることになります。
さらにRatioに対して75日、200日の移動平均線を追加するとこのようになります。
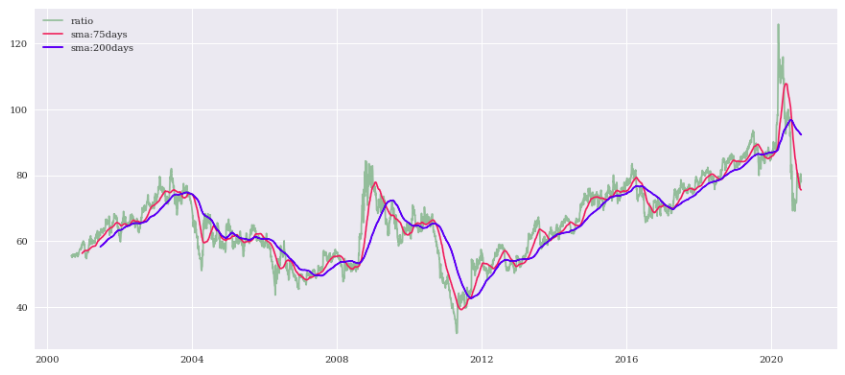
75日線が200日線を上から下に突き抜けているので、今後は下落トレンドになりそうです。
つまり、銀が上がる可能性があります。
いまは資産時代なので銀の保有をおすすめします

ちなみに余談ですが、2008年からアメリカは量的金融緩和を導入しています。
量的金融緩和では米ドルが大量に刷られるため、供給が多くなり、米ドルの価値が低下します。
ここで、マネタリーベースと実質金利の関係を整理しました。
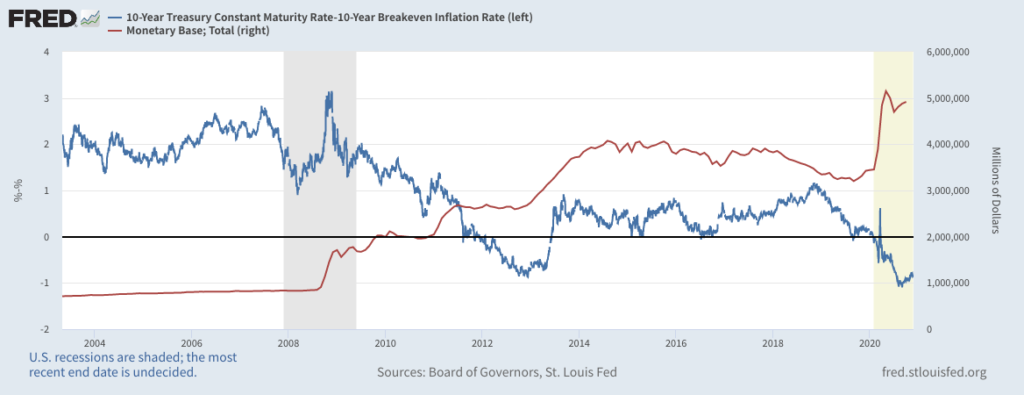
米ドルの急激な増加に伴い、実質金利が低下しています。
なぜ実質金利が下がっているのでしょう?
さらに、マネタリーベースと名目金利(DGS10)、インフレ率(T10YIE)の関係を整理しました。
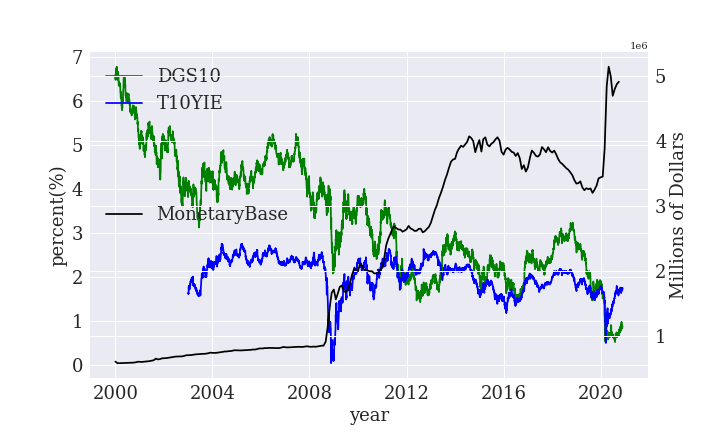
あきらかに名目金利が低下しています。
米国債の利回りがインフレ率を下回っているので、米国債より物(=資産)を持っていたほうが得です。
これからはお金より資産の時代といえます。
銀へのおすすめの投資方法は?

個人投資家が銀に投資する方法はいくつかあります。
(参考:銀に投資する方法は?)
純銀積立と銀ETFのコストは、金と同じような計算です。
金投資のコストを計算した記事をご覧ください。
(参考:お得な金投資の方法は?)
銀をポートフォリオに入れよう

一般的に、リスクを分散させるために、投資対象は多いほうがよいとされています。
ただし、相関が高い資産を組み合わせてもリスクは分散できません。
金と銀の相関が高いことはすでに紹介しました。
そうなると、株価と銀の関係も相関が低いでしょう。
まずは銀投資がどれぐらい儲かるのか調べます。
さらに、S&P500と銀を組み合わせた場合、どのようなポートフォリオが最適なのか考えます。
銀投資は儲かる!投資リターンを比較してみよう

まず、S&P500と金、銀の値動きを比較すると、このようになります。
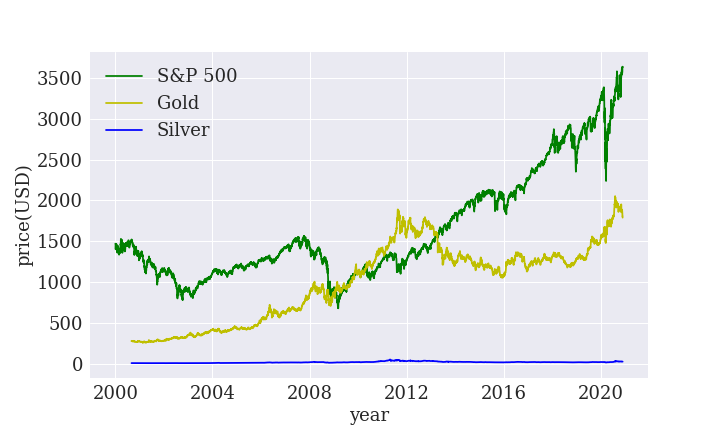
S&P500と金に比べると、銀は直線にしか見えません。
実は、銀は金と比べて非常に安価です。
1オンス当たり20ドル台程度です。
しかし、リターンを見ると面白いことがわかります。
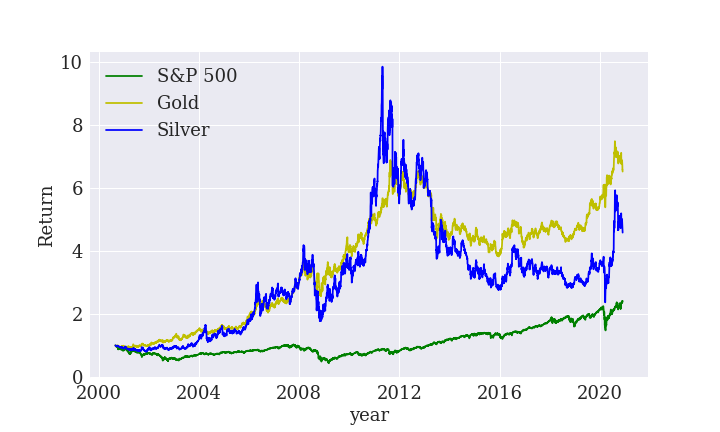
Y軸のリターンは、2000年1月1日の価格を基準に何倍になったかを示しています。
銀は金より値動きがかなり激しく、リターンも大きくなっています。
2000年を基準にすると、2011年には10倍にもなっています。
銀投資はハイリスクハイリターンといえます。
銀の投資比率はどうする?プログラムで試算した結果

S&P500と銀に投資する場合の最適な比率を考えます。
株価と銀の価格は、どちらも変動率が正規分布に従いませんが、参考までに効率的フロンティアを作成します。
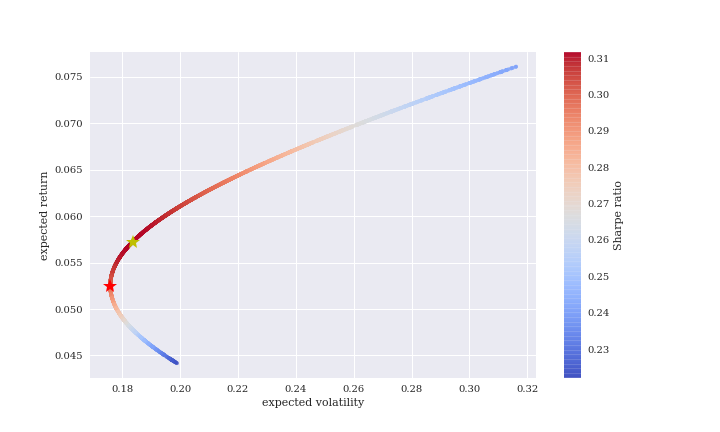
左端に効率的フロンティア曲線を描きました。
赤色星は最もリスクが小さくなる点です。
構成比率は以下になります。
- 期待リターン:5.7%
- 期待ボラリティ:18.4%
- S&P500:59%
- 銀:41%
次にシャープレシオが最も高い点(黄色星)を見ます。
シャープレシオは、期待リターンを期待ボラリティで割ったものです。
- 期待リターン:5.3%
- 期待ボラリティ:17.6%
- S&P500:73.9%
- 銀:26.1%
あくまで参考程度ですが、ぜひ投資の参考にしてください!
まとめ
今回は銀投資を説明しました。
金と同じく、銀もインフレ対策や分散投資に有用なので、ぜひ投資対象に入れましょう。
ここまで読んでくださりありがとうございました。
投資分析に使用したpythonコード

今回使用したPythonコードを以下に示します。
投資とプログラミングの組み合わせに興味があればぜひ活用してください!
相関の調査をpythonで調べる方法

金と銀の価格について、変動率をlogで計算して散布図にプロットしています。
#import libraries
from pandas_datareader import data
import pandas as pd
from pylab import mpl, plt
import numpy as np
import datetime
plt.style.use('seaborn')
mpl.rcParams['font.family'] = 'serif'
%matplotlib inline
#date
start = '2000-01-01'
end = datetime.date.today()
#get price data from Yahoo! finance
def price_df(item, start, end):
file = data.DataReader(item, 'yahoo', start, end)
date = file.index
price = file['Close']
return date, price
#gold
gold_date, gold_price = price_df('GC=F', start, end)
#silver
silver_date, silver_price = price_df('SI=F', start, end)
#make a DataFrame
df = pd.DataFrame()
df['gold'] = gold_price
df['silver'] = silver_price
#calculate log_returns
rets = np.log(df / df.shift(1)).dropna(inplace=True)
#OLS analysis
reg = np.polyfit(rets['silver'], rets['gold'], deg=1)
#make a scatter
ax = rets.plot(kind='scatter', x='silver', y='gold', figsize=(10,6), fontsize=18)
ax.plot(rets['silver'], np.polyval(reg, rets['silver']), 'r', lw=2)
plt.xlabel('Silver', fontsize=18)
plt.ylabel('Gold', fontsize=18)
plt.savefig("silver_gold_1.png")
#correlation
rets.corr()経済データと銀の価格との関係をpythonで調べる方法

FREDから名目金利とインフレ率を取得し、実質金利を計算します。
そのあと、銀の価格と比較グラフを作成します。
#get DGS10 from FRED
tx = data.DataReader('DGS10', 'fred', start, end).dropna()
#get T10YIE from FRED
ty = data.DataReader('T10YIE', 'fred', start, end).dropna()
# calculate real interest rate
test = tx['DGS10'] - ty['T10YIE']
test = test.dropna()
test_date = test.index
#show a graph
fig, ax1 = plt.subplots(figsize=(10, 6))
plt.plot(test_date, test, label = 'DGS10-T10YIE', color='g')
plt.legend(loc=2, fontsize=18)
plt.xlabel('year', fontsize=18)
plt.ylabel('percent(%)', fontsize=18)
plt.tick_params(labelsize=18)
ax2 = ax1.twinx()
plt.plot(silver_date, silver_price, label = 'Silver', color='b')
plt.legend(loc=6, fontsize=18)
plt.ylabel('Silver price(USD)', fontsize=18)
plt.tick_params(labelsize=18)
plt.savefig("silver2.png")経済データをpythonで分析する方法

FREDから名目金利やインフレ率、マネタリーベースを取得してグラフ化しています。
#DGS10
DGS10 = tx['DGS10']
DGS10_date = tx.index
#T10YIE
T10YIE = ty['T10YIE']
T10YIE_date = ty.index
#monetary basa total
tz = data.DataReader('BOGMBASE', 'fred', start, end).dropna()
BOGMBASE_date = tz.index
BOGMBASE = tz['BOGMBASE']
#show a economic analysis
fig, ax1 = plt.subplots(figsize=(10, 6))
plt.plot(DGS10_date, DGS10, label = 'DGS10', color='g')
plt.plot(T10YIE_date, T10YIE, label = 'T10YIE', color='b')
plt.legend(loc=2, fontsize=18)
plt.xlabel('year', fontsize=18)
plt.ylabel('percent(%)', fontsize=18)
plt.tick_params(labelsize=18)
ax2 = ax1.twinx()
plt.plot(BOGMBASE_date, BOGMBASE, label = 'MonetaryBase', color='black')
plt.legend(loc=6, fontsize=18)
plt.ylabel('Millions of Dollars', fontsize=18)
plt.tick_params(labelsize=18)
plt.savefig("silver3.png")価格チャートをpythonで作成する方法

Yahoo! financeより価格データを取得して、グラフ化します。
#S&P 500
SP500_date, SP500_price = price_df('^GSPC', start, end)
#show a price chart
fig, ax1 = plt.subplots(figsize=(10, 6))
plt.plot(SP500_date, SP500_price, label = 'S&P 500', color='g')
plt.plot(gold_date, gold_price, label = 'Gold', color='y')
plt.plot(silver_date, silver_price, label = 'Silver', color='b')
plt.legend(loc=2, fontsize=18)
plt.xlabel('year', fontsize=18)
plt.ylabel('price(USD)', fontsize=18)
plt.tick_params(labelsize=18)
plt.savefig("silver4.png")リターンの比較チャートをpythonで作成する方法

対数収益率でリターンを計算しています。
最初の値を基準にloge(Pn/Pn-1)で計算します。
合計は、loge(Pn/P1)となります。
これをexpの指数に入れることで、Pn/P1が得られます。
つまりリターンは、最初の値の倍数になります。
#make a DataFrame
df = pd.DataFrame()
df['gold'] = gold_price
df['silver'] = silver_price
df['SP500'] = SP500_price
df = df.dropna()
#calculate returns
rets = np.log(df / df.shift(1))
date = df.index
gold_return = rets['gold'].cumsum().apply(np.exp)
silver_return = rets['silver'].cumsum().apply(np.exp)
SP500_return = rets['SP500'].cumsum().apply(np.exp)
#show a return graph
plt.figure(figsize=(10, 6))
plt.plot(date, SP500_return, label = 'S&P 500', color='g')
plt.plot(date, gold_return, label = 'Gold', color='y')
plt.plot(date, silver_return, label = 'Silver', color='b')
plt.legend(loc=2, fontsize=18)
plt.xlabel('year', fontsize=18)
plt.ylabel('Return', fontsize=18)
plt.tick_params(labelsize=18)
plt.savefig("silver5.png")効率的フロンティアをpythonで作成する方法

今回は投資先が2つだったので、曲線になりました。
銀とS&P500の比率を変えて、リスクとリターンの関係を調べています。
シャープレシオは、期待リターンを期待ボラリティで割ったもので、投資効率の指標です。
シャープレシオが高い(赤色が濃い)ほど、効率のよい投資ができます。
#import libraries
import math
import scipy.stats as scs
import statsmodels.api as sm
import scipy.optimize as sco
#number of symbols
noa = 2
#calculate return
def port_ret(weights):
return np.sum(rets.mean() * weights) * 252
#calculate volatility
def port_vol(weights):
return np.sqrt(np.dot(weights.T, np.dot(rets.cov() * 252, weights)))
#calculate plot data
prets = []
pvols = []
for p in range(2500):
weights = np.random.random(noa)
weights /= np.sum(weights)
prets.append(port_ret(weights))
pvols.append(port_vol(weights))
prets = np.array(prets)
pvols = np.array(pvols)
#calculate sharp ratio
def min_func_sharpe(weights):
return -port_ret(weights) / port_vol(weights)
#restriction
cons = ({'type':'eq', 'fun':lambda x: np.sum(x) - 1})
bnds = tuple((0, 1) for x in range(noa))
#start point
eweights = np.array(noa * [1. / noa,])
#calculate the best sharp ratio
%%time
opts = sco.minimize(min_func_sharpe, eweights,
method='SLSQP', bounds=bnds,
constraints=cons)
#the result of calculation
opts['x'].round(3)
port_ret(opts['x']).round(3)
port_vol(opts['x']).round(3)
#calculate minimum volatility
optv = sco.minimize(port_vol, eweights,
method='SLSQP', bounds=bnds,
constraints=cons)
#the result of calculation
optv['x'].round(3)
port_vol(optv['x']).round(3)
port_ret(optv['x']).round(3)
#show a efficient frontier
plt.figure(figsize=(10, 6))
plt.scatter(pvols, prets, c=prets / pvols,
marker='.', alpha=0.8, cmap='coolwarm')
plt.plot(port_vol(opts['x']), port_ret(opts['x']),
'y*', markersize=15.0)
plt.plot(port_vol(optv['x']), port_ret(optv['x']),
'r*', markersize=15.0)
plt.xlabel('expected volatility')
plt.ylabel('expected return')
plt.colorbar(label='Sharpe ratio')
plt.savefig("silver7.png");投資とプログラミングの組み合わせに興味があれば、ぜひ声をかけてくださいね。
ここまで読んでくださりありがとうございました。^^
★pythonによる投資の分析を学ぶのにおすすめの本

