○この記事で伝えたいこと
- 仮想通貨への投資はハイリスクハイリターン。
- Pythonを使えば価格分析がとっても楽にできる。
- 投資効率を求めるならビットコイン1本でいこう。
こんにちはー、ウチダです!
ぼくは経済や金融、投資が好きで、いまは投資とプログラミングの組み合わせを勉強しています。
今回は仮想通貨への投資効率を最大化するためにデータ分析をした話をします。
目次
仮想通貨への投資

2020年11月中旬、仮想通貨が全面高となりました。
ぼくは2019年7月から仮想通貨を数十万円保有しており、含み益が大きくなっています。
今回は仮想通貨への投資効率を最大化するために、プログラミングで価格データの分析を行いました。
仮想通貨とは?

仮想通貨(暗号資産)とは、インターネットを通じて電子的な決済手段に用いられる通貨です。
国が発行している通貨(円、米ドルなど)とは異なります。(参考:仮想通貨とは?)
有名な仮想通貨だと、ビットコイン(BTC)やイーサリアム(ETH)が挙げられます。
仮想通貨は儲かるの?

仮想通貨は1通貨当たりの価格が常に動いています。
価格の変動は非常に大きく、数時間で10%以上動くこともあります。
その分、大きなリターンも狙うことができ、ハイリスク・ハイリターンの投資です。
将来的な価値には強気派と弱気派がおり、意見が分かれています。
強気派は将来数十倍に上がると主張しており、大きなリターンが期待されています(参考:ビットコインは将来いくらになる?)
おすすめの投資スタイルは?

ぼくは長期投資をおすすめします。
仮想通貨は24時間365日レートが動いており、さらに数時間で10%以上動くこともあります。
毎日の値動きに対応するのは、かなり体力が必要になります。
また、将来的な価値が明確でないため、大金を入れるのは危険です。
したがって、少額を投資してほったらかしにする長期投資がよいと考えています。
プログラミングで価格チャートを作成

ぼくは経済や金融、投資が好きで、いまは投資とプログラミングの組み合わせを独学しています。
プログラミング言語はPythonを使用しています。
Pythonとは?

Pythonはデータ分析、AI、機械学習、深層学習といった分野で主要言語となっています。
コードがシンプルで読み書きしやすい特徴から、初学者でも勉強しやすいプログラミング言語です。
さらに、Pythonは外部ライブラリが使えるため、天才たちが作ってくれたライブラリをインストールすれば、自分のプログラムで自由に使えます。
今回はyahoo! financeから仮想通貨の価格データを取得してチャートを作成しました。(参考:yahoo! finance)
価格チャートを表示する

仮想通貨にはBTC、ETH、XRP、BCH、LTCを選び、レートは米ドルで取得しました。
期間は2017年7月30日から2020年11月23日です。
価格は終値(Close)を採用しています。
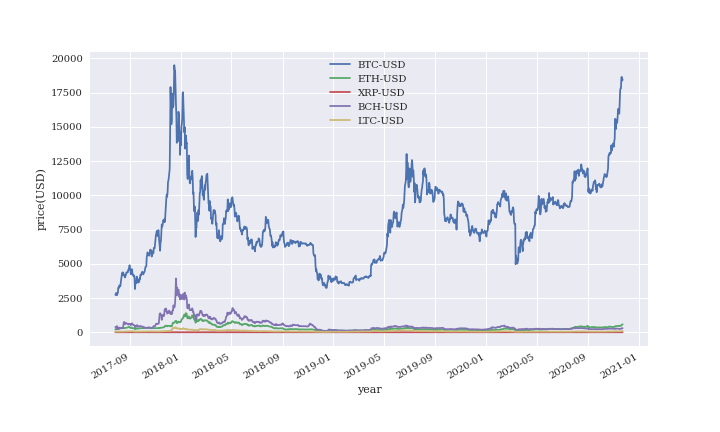
仮想通貨の中でビットコインの価格が飛び抜けて高いです。
他の仮想通貨が直線にしか見えません。
そこで、価格を表で示します。
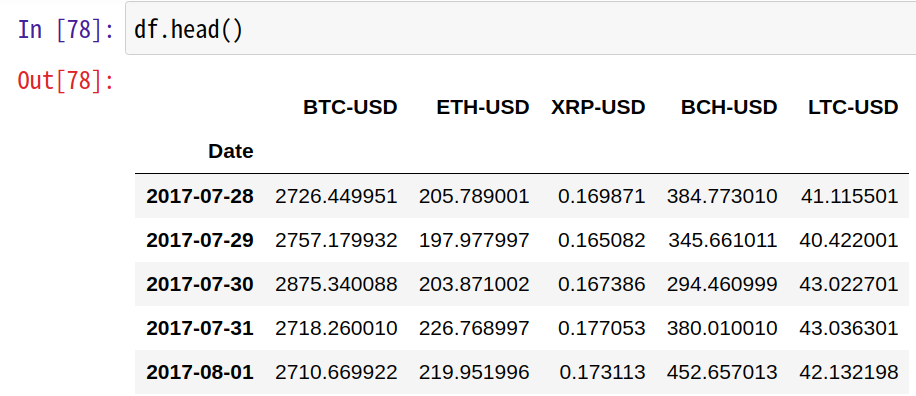
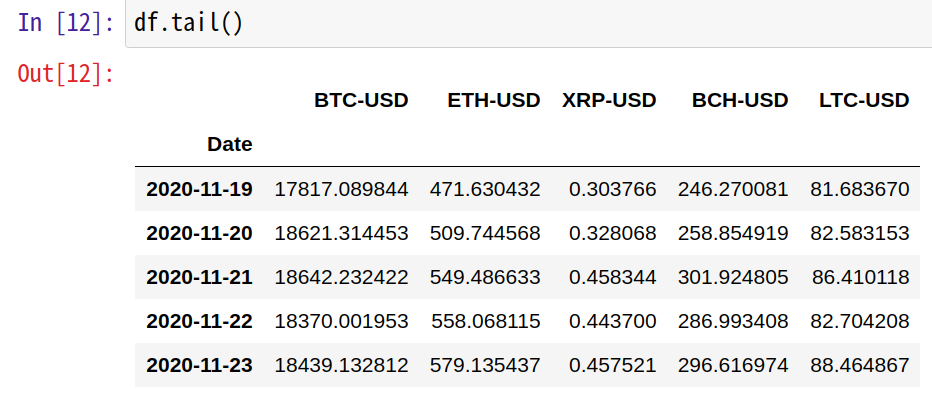
ビットコインを見ると、2017年7月末から2020年11月中旬にかけて約7倍にもなっています。
当初100万円投資していたら、700万円ですよ!
素晴らしいリターンです。
ただ、価格チャートを見ると、単純な直線では上昇していません。
また、他の仮想通貨も、価格は小さいものの、7倍以上に増えている可能性もあります。
そこで、対数収益率を使って、リターンをグラフ化します。
リターンを比較する

対数収益率は、リターンの計算に使用されます。(参考:対数収益率とは?)
今回は2017年7月末の価格を基準にして、リターンを計算しました。
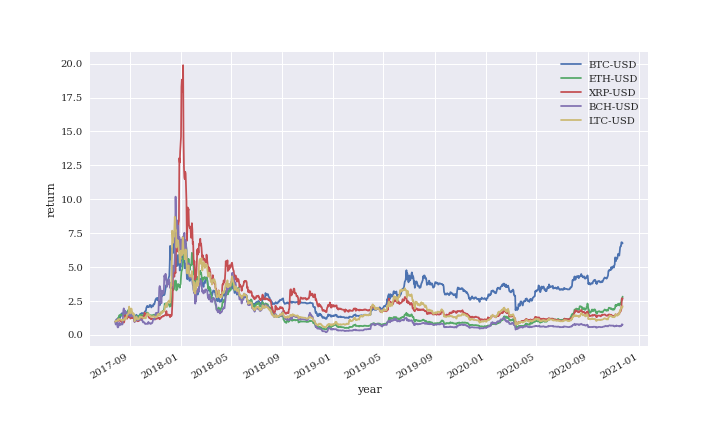
縦軸は、基準の価格から何倍になったかを示しています。
2018年ごろが仮想通貨バブルです。
XRPは20倍のリターンをたたき出しています。
当初100万円投資していたら、2000万円。
老後不安も一気に解消です。(実際は税金がかかります)
バブル以降の値動きはどうでしょう?
見づらいので、グラフをバブルが落ち着いた時期(2019年1月1日)からに直します。
基準の価格は2017年7月末のままです。
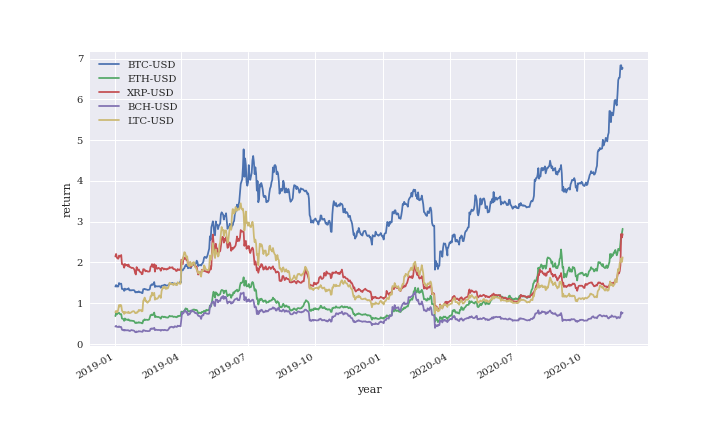
いずれも2019年7月に再度上昇し、そのあと2019年3月のコロナショックまでやや下落傾向でした。
それ以降、BTCが急上昇しています。
また、ETH、XRP、LTCが上昇し始めています。
(BCHどうした、がんばれ!)
2020年10月から大きな上昇局面に入ったので、今後の動向に注目です。
プログラミングで仮想通貨のポートフォリオをつくる

投資効率を最大化するために、仮想通貨のポートフォリオを効率的フロンティアで作ります。
効率的フロンティアはあくまで過去の実績を基に作成します。
また、価格の変動が正規分布に従う前提があるので、今回は参考程度にしてください。
なお、データは2019年1月1日以降にします。
まず仮想通貨の価格の変動が正規分布に従うのか調べます。
価格の変動が正規分布か調べる

今回はQQプロットを用いてBTCの価格変動が正規分布になっているのか調べます。(参考:QQプロットとは?)
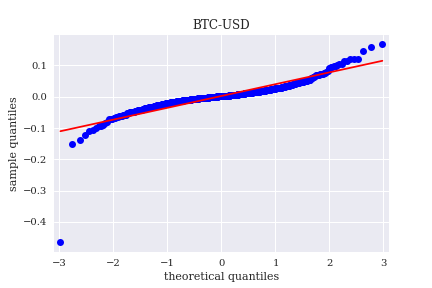
青色の点が、赤い直線にピタリと沿えば正規分布といえます。
しかし、BTCは形が歪で、正規分布とはいえません。
他の仮想通貨も同様でした。
したがって、効率的フロンティアは前提が崩れた状態で作成します。
あくまで参考程度に。
リスクとリターンの関係を調べる

効率的フロンティアは、同じリターンを求める時、最小のリスクになる点を結んで得られる曲線です。
イメージはこんなやつです。
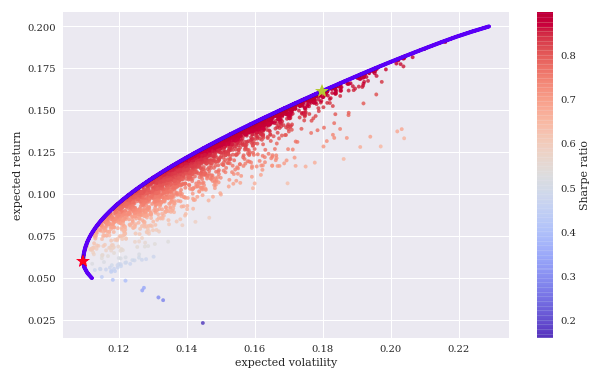
この青い曲線が効率的フロンティアです。
この曲線上の点を取るポートフォリオを作成することで、効率的な投資ができます。
では、さっそく仮想通貨のリスクとリターンの関係を調べます。
仮想通貨にはBTC、ETH、XRPを使いました。
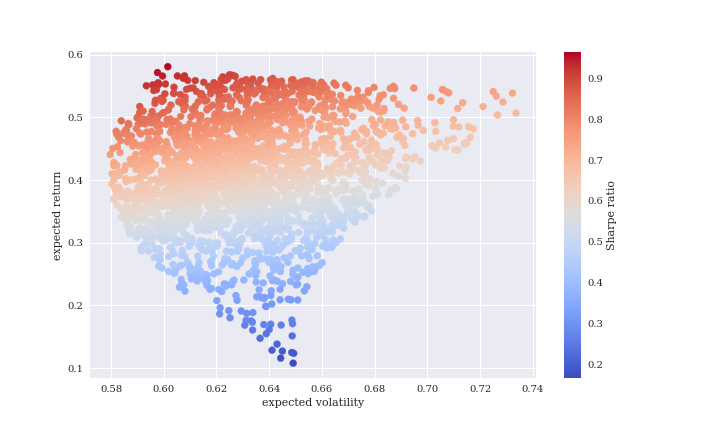
左側に扇が広がったような形になりました。
リスクもリターンも値がすごく大きいです。
ここに効率的フロンティアを描きます。
効率的フロンティアを描く

扇の左端に沿うように効率的フロンティアを描きました。
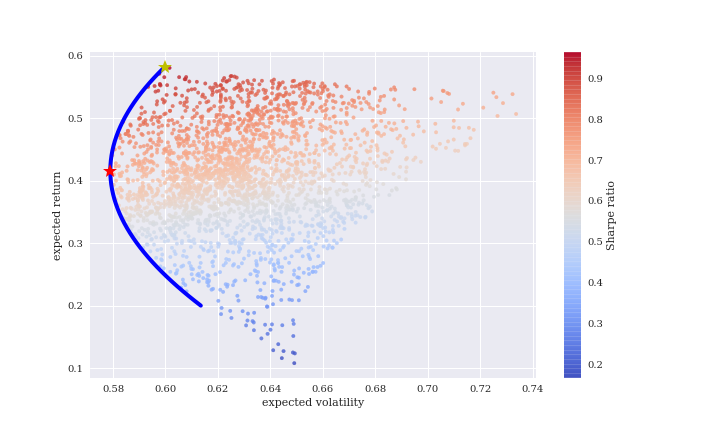
赤色星は最もリスクが小さくなる点です。
構成比率は以下になります。
- 期待リターン:41.6%
- 期待ボラリティ:57.9%
- BTC:65.5%
- ETH:なし
- XRP:34.5%
次にシャープレシオが最も高い点(黄色星)を見ます。
シャープレシオは、期待リターンを期待ボラリティで割ったものです。
投資効率の指標であり、大きいほど効率がいいです。
- 期待リターン:58.3%
- 期待ボラリティ:60%
- BTC:100%
- ETH:なし
- XRP:なし
シャープレシオを最大化したいなら、BTC1本にかけなさいと笑。
あくまで参考程度です。
ただ、これから仮想通貨への投資を始めるなら、BTC1本でいいかもしれません。
使用したプログラムのコード

今回使用したPythonコードを以下に示します。
環境構築は必要ですが、お役に立てると嬉しいです。
なお、ぼくのOSはUbuntu20.04.1 LTSで、プログラムはjupyter notebookで使用しました。
価格チャートを表示する

yahoo! financeから価格データを取得します。
日付は、yahoo! financeのヒストリカルデータを参考に変更してください。
#import libraries
from pandas_datareader import data
import pandas as pd
from pylab import mpl, plt
import numpy as np
import datetime
plt.style.use('seaborn')
mpl.rcParams['font.family'] = 'serif'
get_ipython().run_line_magic('matplotlib', 'inline')
#make a DataFrame
df = pd.DataFrame()
#get price data from yahoo finance
def price_df(crypto, start, end):
file = data.DataReader(crypto, 'yahoo', start, end)
df['%s' % crypto] = file['Close']
#symbols of cryptocurrency
symbols = ['BTC-USD', 'ETH-USD', 'XRP-USD', 'BCH-USD', 'LTC-USD']
#date
start = '2019-01-01'
end = datetime.date.today()
#run to get price data
for sym in symbols:
price_df(sym, start, end)
#check df as table
df.head()
df.tail()
#show a price chart
df.dropna().plot(figsize=(10, 6))
plt.legend(loc=0)
plt.xlabel('year')
plt.ylabel('price(USD)')
plt.savefig("crypto1.png")リターンを比較する

最初の値を基準にloge(Pn/Pn-1)で計算します。
合計は、loge(Pn/P1)となります。
これをexpの指数に入れることで、Pn/P1が得られます。
つまりリターンは、最初の値の倍数になります。
#calculate
rets = np.log(df / df.shift(1))
#show a return chart
rets.cumsum().apply(np.exp).plot(figsize=(10, 6))
plt.legend(loc=0)
plt.xlabel('year')
plt.ylabel('return')
plt.savefig("cypto2.png")
#show a return chart from 2019-01-01
rets.cumsum().apply(np.exp).loc['2019-01-01':].plot(figsize=(10, 6))
plt.legend(loc=0)
plt.xlabel('year')
plt.ylabel('return')
plt.savefig("cypto3.png")正規分布か調べる

QQプロットを使った調査です。
赤色の直線にデータが沿えば、正規分布だと判定できます。
import libraries
import math
import scipy.stats as scs
import statsmodels.api as sm
#calculate returns
log_returns = np.log(df / df.shift(1))
log_returns.head()
#show a qq plot
sm.qqplot(log_returns['BTC-USD'].dropna(), line='s')
plt.title('BTC-USD')
plt.xlabel('theoretical quantiles')
plt.ylabel('sample quantiles');
plt.savefig("cypto4.png")リスクとリターンの関係を表示する

過去の価格データを基に、標準偏差と平均からプロットします。
今回は2500個の点でプロットしました。
#symbols of cryptocurrency
symbols = ['BTC-USD', 'ETH-USD', 'XRP-USD']
noa = len(symbols)
#get price data
data = df[symbols]
rets = np.log(data / data.shift(1))
#calculate return in a year
def port_ret(weights):
return np.sum(rets.mean() * weights) * 252
#calculate volatility in a year
def port_vol(weights):
return np.sqrt(np.dot(weights.T, np.dot(rets.cov() * 252, weights)))
#make plotting data
prets = []
pvols = []
for p in range(2500):
weights = np.random.random(noa)
weights /= np.sum(weights)
prets.append(port_ret(weights))
pvols.append(port_vol(weights))
prets = np.array(prets)
pvols = np.array(pvols)
#make a risk-return chart
plt.figure(figsize=(10, 6))
plt.scatter(pvols, prets, c=prets / pvols,
marker='o', cmap='coolwarm')
plt.xlabel('expected volatility')
plt.ylabel('expected return')
plt.colorbar(label='Sharpe ratio');
plt.savefig("cypto5.png")効率的フロンティアを表示する

投資効率を最大化する点をなぞります。
optsは、シャープレシオが最大値をとる点です。
optvは、期待ボラリティ(リスク)が最小の点です。
#import libraries
import scipy.optimize as sco
#calculate a sharpe ratio
def min_func_sharpe(weights):
return -port_ret(weights) / port_vol(weights)
#restriction
cons = ({'type':'eq', 'fun':lambda x: np.sum(x) - 1})
bnds = tuple((0, 1) for x in range(noa))
#start point
eweights = np.array(noa * [1. / noa,])
eweights
min_func_sharpe(eweights)
#calculate a maximum sharp ratio
opts = sco.minimize(min_func_sharpe, eweights,
method='SLSQP', bounds=bnds,
constraints=cons)
#show the result
opts
#show the portfolio
opts['x'].round(3)
#show the return
port_ret(opts['x']).round(3)
#show the volatility
port_vol(opts['x']).round(3)
#show the sharpe ratio
port_ret(opts['x']) / port_vol(opts['x'])
#calculate the minimum volatility
optv = sco.minimize(port_vol, eweights,
method='SLSQP', bounds=bnds,
constraints=cons)
#show the result
optv
#show the portfolio
optv['x'].round(3)
#show the volatility
port_vol(optv['x']).round(3)
#show the return
port_ret(optv['x']).round(3)
#show the sharpe ratio
port_ret(optv['x']) / port_vol(optv['x'])
#restriction
cons = ({'type':'eq', 'fun':lambda x: port_ret(x) - tret},
{'type':'eq', 'fun': lambda x: np.sum(x) - 1})
bnds = tuple((0, 1) for x in weights)
#claculate efficient frontier
trets = np.linspace(0.2, 0.58, 50)
tvols = []
for tret in trets:
res = sco.minimize(port_vol, eweights, method='SLSQP',
bounds=bnds, constraints=cons)
tvols.append(res['fun'])
tvols = np.array(tvols)")
#show a efficient frontier chart
plt.figure(figsize=(10, 6))
plt.scatter(pvols, prets, c=prets / pvols,
marker='.', alpha=0.8, cmap='coolwarm')
plt.plot(tvols, trets, 'b', lw=4.0)
plt.plot(port_vol(opts['x']), port_ret(opts['x']),
'y*', markersize=15.0)
plt.plot(port_vol(optv['x']), port_ret(optv['x']),
'r*', markersize=15.0)
plt.xlabel('expected volatility')
plt.ylabel('expected return')
plt.colorbar(label='Sharpe ratio')
plt.savefig("cypto6.png");まとめ
今回は仮想通貨への投資効率を最大化することにチャレンジした話でした。
これらはあくまで過去のデータです。
他のデータ、経済情勢を踏まえて、未来のポジションをとりましょう。
ここまで読んでくださりありがとうございました。
